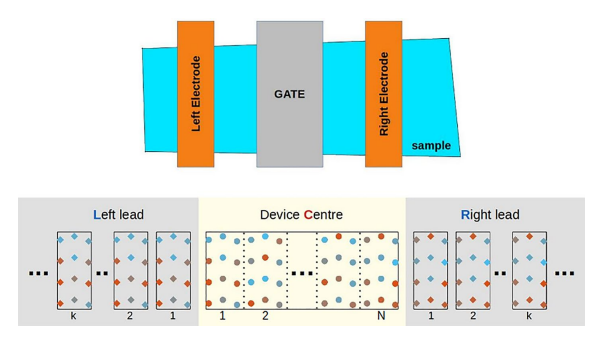
The Green’s function method is recognized to be a very powerful tool for modelling quantum transport in nanoscale electronic devices. As atomistic calculations are generally expensive, numerical methods and related algorithms have been developed accordingly to optimize their computation cost. In particular, recursive techniques have been efciently applied within the Green’s function calculation approach. Recently, with the discovery of Moiré materials, several attractive superlattices have been explored using these recursive Green’s function techniques. However, numerical difculty issues were reported as most of these superlattices have relatively large supercells, and consequently a huge number of atoms to be considered. In this article, improvements to solve these issues are proposed in order to keep optimizing the recursive Green’s function calculations. These improvements make the electronic structure calculations feasible and efcient in modelling large superlattice-based devices. As an illustrative example, twisted bilayer graphene superlattices are computed and presented to demonstrate the efciency of the method.
Recursive Green’s functions optimized for atomistic modelling of large superlattice‑based devices