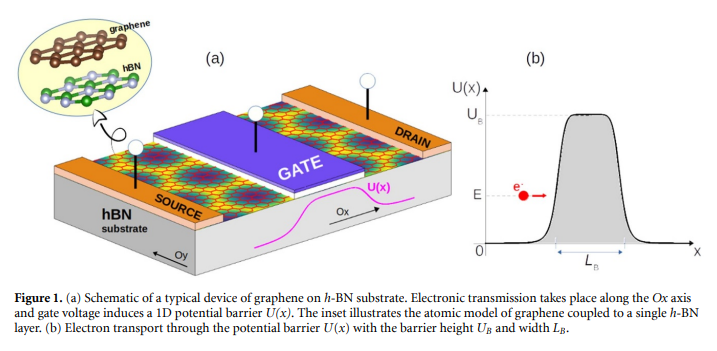
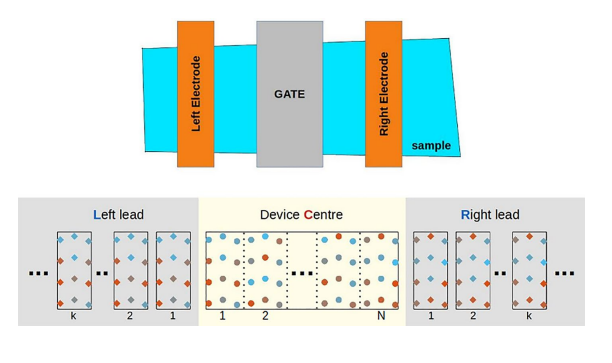
Klein tunneling degradation and enhanced Fabry-Pérotinterference in graphene/h-BN moiré-superlattice devices
Hexagonal boron-nitride (h-BN) provides an ideal substrate for supporting graphene devices to achieve fascinating transport properties, such as Klein tunneling, electron optics and other novel quantum transport phenomena. However, depositing graphene on h-BN creates moiré superlattices, whose electronic properties can be significantly manipulated by controlling the lattice alignment between layers. In this work, the effects of these moiré structures on the transport properties of graphene are investigated using atomistic simulations. At large misalignment angles (leading to small moiré cells), the transport properties (most remarkably, Klein tunneling) of pristine graphene devices are conserved. On the other hand, in the nearly aligned cases, the moiré interaction induces stronger effects, significantly affecting electron transport in graphene. In particular, Klein tunneling is significantly degraded. In contrast, strong Fabry-Pérot interference (accordingly, strong quantum confinement) effects and non-linear I-V characteristics are observed. P-N interface smoothness engineering is also considered, suggesting as a potential way to improve these transport features in graphene/h-BN devices.